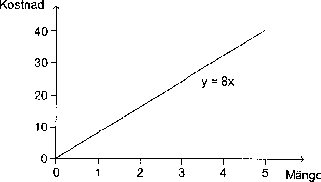funktion
Ett av de allra viktigaste begreppen i matematik. Ordet kommer av ett latinskt ord som betyder fullgöra, utöva.

Vardagligt. En mätbar egenskap som är beroende av en annan mätbar egenskap. De två egenskaperna betecknas vanligen y och x.
Ex: Lufttrycket (y) är en funktion av höjden över havet (x).
Ex: Bromssträckan för en bil (y) är en funktion av hastigheten (x).
Ex: Arean (ytan) av ett cirkelområde (A) är en funktion av radiens längd (r).

Matematiskt sägs y vara en funktion av x om det för varje värde på x finns precis ett värde på y. Man säger att den beroende variabeln y är en funktion av (beror av) den oberoende variabeln x.

Tre sätt att beskriva en funktion
En funktion kan vanligen beskrivas på tre olika sätt: i en värdetabell, som en ekvation och som en graf (en bild). I exemplet nedan ses kostnaden y för ett inköp som en funktion av den inköpta mängden x.

1. Värdetabell (del)
 

	Mängd	Kostnad
	x	y
	0	0
	1	8
	2	16
	3	24
	4	32
	5	40

De x-värden som finns (eller kan finnas) kallas för funktionens definitionsmängd, y-värdena för dess värdemängd.

2. Ekvation
Ekvationen är den formel som ger y-värdet för ett visst x-värde. Det y-värde man får kallas funktionsvärdet. Funktionen ovan kan skrivas som ekvationen

y = 8x

För exempelvis x = 3 får man funktionsvärdet

y = 8·3 = 24

vilket stämmer med y-värdet i värdetabellen ovan.

3. Graf
Av ett grekiskt ord som betyder skriva. En graf är den bild av x-värden och y-värden som man kan rita i ett koordinatsystem. Den är oftast en kurva eller en linje (rak kurva). Men den kan också vara ett antal isolerade punkter; se punktdiagram.

För exemplet under Värdetabell ovan får man linjen y = 8x; se figuren nedan.

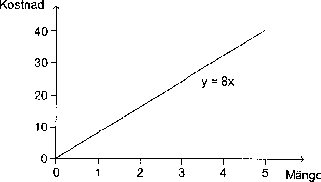
Åter