|
Pythagoras sats [pyta´goras]
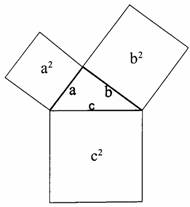
För en rätvinklig tringel är
kvadraten på hypotenusan [hypotenu´sa] lika
med summan av kvadraterna på kateterna (en katet [kate´t], två kateter).
Satsen är uppkallad efter den grekiske filosofen och matematikern
Pythagoras (ca 570–497 f.Kr.) och är en av de mest berömda satserna i
matematikens historia. Den kan bevisas på ett stort antal olika sätt.
Ordet hypotenusa kommer av ett grekiskt ord som betyder sträcka sig under
och ordet katet av ett likaledes grekiskt ord som betyder lodlinje.
Om hypotenusan kallas c och kateterna a och b gäller att
c2
= a2
+ b2
Ex: I en rätvinklig triangel är kateterna 4 cm och 6 cm. Man får att
hypotenusan =
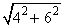 cm
= cm
= 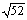 cm
» 7,2 cm cm
» 7,2 cm
Ex: I en annan rätvinklig triangel är den ena kateten 8 dm och
hypotenusan 15 dm. Man får att
den andra kateten =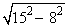 dm
= dm
= 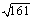 dm
» 12,7 dm dm
» 12,7 dm
Se också egyptisk triangel.
Åter |
