kon
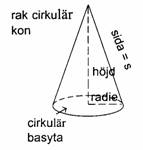
Kropp som begränsas av en mantelyta och en basyta. Vanligen menas en s.k. rak cirkulär kon. En sådan kon kallas rak därför att höjden går från basytans mittpunkt och cirkulär därför att basytan är ett cirkelområde. Orden kon och mantel kommer av två latinska ord som betyder kägla respektive hölje.

Ex:

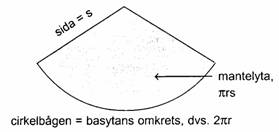
Höjden av en rak cirkulär kon är den sträcka som har ena ändpunkten i spetsen och den andra i basytans medelpunkt. Sidan är varje sträcka som har ena ändpunkten i konens spets och den andra på den cirkel som omger basytan.
    Vanliga formler för volymen V och mantelytans area A är

V = pr²h/3      A = prs

där p (pi) är ett tal ungefär lika med 3,14, r är radien i en cirkulär basyta, h är konens höjd och s är dess sida. Mer om p finns under pi.
    pr²h/3 (pi r två h genom tre) ska tolkas som p·r·r·h/3 och prs (pi r s) som p·r·s.

Ex: En glasstrut har invändigt radien 2 cm, höjden 8 cm och sidan ca 8,2 cm. Man får att volymen respektive arean av (den invändiga) mantelytan är

V » 3,14·2·2·8/3 cm³ » 33,5 cm³ (kubikcentimeter) och
A » 3,14·2·8,2 cm² » 51,5 cm² (kvadratcentimeter)

Anm: Känner man höjden och radien i en rak cirkulär kon kan man beräkna sidan s med hjälp av Pythagoras sats [pyta´goras], I exemplet får man att

s² = 2² + 8², som ger s » 8,2

Åter